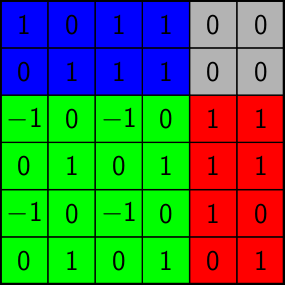
A matrix $M \in \{0,1\}^{m \times n}$ has the consecutive ones property for columns if there is a permutation of the columns such that the permuted matrix $M' \in \{0,1\}^{m \times n}$ has the $1$'s of each row consecutive. Similarly, $M \in \{0,1\}^{m \times n}$ has the consecutive ones property for rows if $M^{\mathsf{T}}$ has the consecutive ones property for columns.