Graphic / Cographic / Planar Matrices

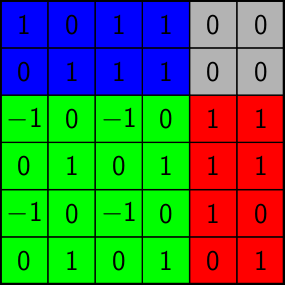
Let \( G = (V,E) \) be a graph and let \( T \) be a spanning forest. The matrix \( M(G,T) \in \{0,1\}^{T \times (E \setminus T)} \) defined via

\[ M(G,T)_{e,f} := \begin{cases} 1 & \text{if } e \text{ is contained in the unique cycle of } T \cup \{f\} \\ 0 & \text{otherwise} \end{cases} \]

is called the graphic matrix of \( G \) with respect to \( T \). A binary matrix \( M \) is called graphic if there exists a graph \( G \) with a spanning forest \( T \) such that \( M = M(G,T) \). Moreover, \( M \) is called cographic if \( M^{\textsf{T}} \) is graphic, and it is called planar if it is graphic and cographic.

Recognizing Graphic Matrices

The command

cmr-graphic IN-MAT [OPTION]...

determines whether the matrix given in file IN-MAT is (co)graphic.

Options:

• -i FORMAT Format of file IN-MAT; default: dense.
• -t Test for being cographic; default: test for being graphic.
• -G OUT-GRAPH Write a graph to file OUT-GRAPH; default: skip computation.
• -T OUT-TREE Write a spanning tree to file OUT-TREE; default: skip computation.
• -D OUT-DOT Write a dot file OUT-DOT with the graph and the spanning tree; default: skip computation.

Advanced options:

• --stats Print statistics about the computation to stderr.
• --time-limit LIMIT Allow at most LIMIT seconds for the computation.

Formats for matrices: dense, sparse

If IN-MAT is - then the matrix is read from stdin.

If OUT-GRAPH, OUT-TREE, OUT-DOT or NON-SUB is - then the graph (resp. the tree, dot file or non-(co)graphic submatrix) is written to stdout.

Algorithm

The implemented recognition algorithm is based on An Almost Linear-Time Algorithm for Graph Realization by Robert E. Bixby and Donald K. Wagner (Mathematics of Operations Research, 1988). For a matrix \( M \in \{0,1\}^{m \times n}\) with \( k \) nonzeros it runs in \( \mathcal{O}( k \cdot \alpha(k, m) ) \) time, where \( \alpha(\cdot) \) denotes the inverse Ackerman function.

C Interface

The corresponding functions in the library are

• CMRgraphicTestMatrix() tests a matrix for being graphic.
• CMRgraphicTestTranspose() tests a matrix for being cographic.

and are defined in network.h.

Computing graphic matrices

The command

cmr-graphic -c IN-GRAPH OUT-MAT [OPTION]...

computes a (co)graphic matrix corresponding to the graph from file IN-GRAPH and writes it to OUT-MAT.

Options:

• -o FORMAT Format of file OUT-MAT; default: dense.
• -t Return the transpose of the graphic matrix.
• -T IN-TREE Read a tree from file IN-TREE; default: use first specified arcs as tree edges.

Advanced options:

• --stats Print statistics about the computation to stderr.
• --time-limit LIMIT Allow at most LIMIT seconds for the computation.

Formats for matrices: dense, sparse

If IN-GRAPH or IN-TREE is - then the graph (resp. tree) is read from stdin.

If OUT-MAT is - then the matrix is written to stdout.

C Interface

The corresponding function in the library is

• CMRgraphicComputeMatrix() constructs a graphic matrix for a given graph.

and is defined in network.h.