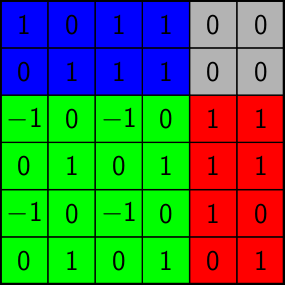
A key tool for the recognition of network matrices, totally unimodular matrices and balanceable matrices is Camion's signing algorithm. Its input is a binary matrix \( M \in \{0,1\}^{m \times n} \) and it computes a ternary matrix \( M' \in \{-1,0,+1\}^{m \times n} \) with the same support, i.e., the same nonzero entries. The output matrix \( M' \) is guaranteed to be balanced if (and only if) \( M \) was balanceable. This means that for every square submatrix of \( M' \) with two nonzero entries per row and per column the the sum of all entries is divisible by 4. The algorithm always outputs a Camion-signed matrix, regardless of whether the input matrix was balanceable. In particular, it does not recognize whether it deals with a balanceable matrix or not.

If \( M \) is balanceable, then \( M' \) is unique up to scaling rows/columns with \( -1 \).

Checking for being Camion-signed

The command

cmr-camion IN-MAT [OPTION]...

determines whether the matrix given in file IN-MAT is Camion-signed.

Options:

-i FORMAT Format of file IN-MAT; default: dense.
-N NON-SUB Write a minimal non-Camion submatrix to file NON-SUB; default: skip computation.

Advanced options:

--stats Print statistics about the computation to stderr.
--time-limit LIMIT Allow at most LIMIT seconds for the computation.

Formats for matrices: dense, sparse If IN-MAT is - then the matrix is read from stdin. If NON-SUB is - then the submatrix is written to stdout.

Algorithm

The implemented recognition algorithm is based on Section 18 of A decomposition theory for matroids. V. Testing of matrix total unimodularity by Klaus Truemper (Journal of Combinatorial Theory, Series B, 1990). For a matrix \( M \in \{-1,0,1\}^{m \times n} \) it runs in \( \mathcal{O}( \min(m^2 \cdot n, m \cdot n^2) ) \) time.

C Interface

The corresponding function in the library is

CMRcamionTestSigns() tests a matrix for being Camion-signed.

and is defined in camion.h.

Camion-signing a Matrix

The command

cmr-camion IN-MAT -S OUT-MAT [OPTION]...

modifies the signs of the matrix given in file IN-MAT such that it is Camion-signed and writes the resulting new matrix to file OUT-MAT.

Options:

-i FORMAT Format of file IN-MAT; default: dense.
-o FORMAT Format of file OUT-MAT; default: same as format of IN-MAT.

Advanced options:

--stats Print statistics about the computation to stderr.
--time-limit LIMIT Allow at most LIMIT seconds for the computation.

Formats for matrices: dense, sparse If IN-MAT is - then the matrix is read from stdin. If OUT-MAT is - then the matrix is written to stdout.

Algorithm

The implemented algorithm is based on Section 18 of A decomposition theory for matroids. V. Testing of matrix total unimodularity by Klaus Truemper (Journal of Combinatorial Theory, Series B, 1990). For a matrix \( M \in \{-1,0,1\}^{m \times n} \) it runs in \( \mathcal{O}( \min(m^2 \cdot n, m \cdot n^2) ) \) time.

C Interface

The corresponding function in the library is

CMRcamionComputeSigns() Computes a Camion-signed version of a given ternary matrix.

and is defined in camion.h.