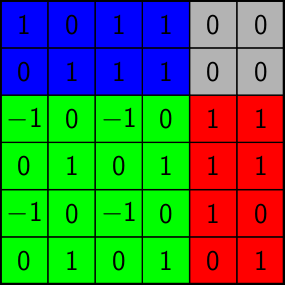
A matrix \( M \in \mathbb{Z}^{m \times n} \) is totally unimodular if all its square submatrices have a determinant in \( \{-1,0,+1\} \). Here, a submatrix does not need to be contiguous, i.e., the matrix \(M = \begin{pmatrix} 1 & 0 & -1 \\ 1 & 0 & 1 \end{pmatrix} \) is not totally unimodular since the submatrix indexed by rows \( \{1, 2 \} \) and columns \( \{ 1,3 \} \) has determinant 2. In particular, every totally unimodular matrix has only entries in \( \{-1,0,+1\} \) as these are the 1-by-1 submatrices.

Recognizing Totally Unimodular Matrices

The command

cmr-tu IN-MAT [OPTION...]

determines whether the matrix given in file IN-MAT is totally unimodular.

Options:

-i FORMAT Format of file IN-MAT; default: dense.
-D OUT-DEC Write a decomposition tree of the underlying regular matroid to file OUT-DEC; default: skip computation.
-N NON-SUB Write a minimal non-totally-unimodular submatrix to file NON-SUB; default: skip computation.

Advanced options:

--stats Print statistics about the computation to stderr.
--time-limit LIMIT Allow at most LIMIT seconds for the computation.
--no-direct-graphic Check only 3-connected matrices for regularity.
--no-series-parallel Do not allow series-parallel operations in decomposition tree.
--naive-submatrix Use naive bad submatrix algorithm instead of greedy heuristic.
--algo ALGO Use algorithm from {decomposition, submatrix, partition}; default: decomposition.

Formats for matrices: dense, sparse If IN-MAT is - then the matrix is read from stdin. If OUT-DEC or NON-SUB is - then the decomposition tree (resp. the submatrix) is written to stdout.

Algorithms

The implemented default recognition algorithm is based on Implementation of a unimodularity test by Matthias Walter and Klaus Truemper (Mathematical Programming Computation, 2013). It either runs Camion's Signing Algorithm to reduce the question to that of recognizing binary regular matroids or decomposes a given ternary matrix directly by means of a Seymour decomposition. Please cite the paper in case the implementation contributed to your research:

@Article{WalterT13,
  author    = {Walter, Matthias and Truemper, Klaus},
  title     = {Implementation of a unimodularity test},
  journal   = {Mathematical Programming Computation},
  year      = {2013},
  volume    = {5},
  number    = {1},
  pages     = {57--73},
  issn      = {1867-2949},
  doi       = {10.1007/s12532-012-0048-x},
  publisher = {Springer-Verlag},
}

In order to repeat experiments described in the paper above, the function can be parameterized as to use exponential-time algorithms.

The first is based on the criterion of Ghouila-Houri and runs in time \( \mathcal{O}( (m + n) \cdot 3^{\min(m, n)}) \).
The second enumerates square Eulerian submatrices and runs in time \( \mathcal{O}( (m+n) \cdot 2^{ m + n } ) \).

C Interface

The corresponding function in the library is

CMRtuTest() tests a matrix for being totally unimodular.

and is defined in tu.h. Its parameters also allow to choose one of the enumeration algorithms with exponential running time instead of the decomposition algorithm.